2 つのエージェントのチャットは最も単純な会話パターン形式です。各々の ConversableAgent エージェントの initiate_chat メソッドを使用して 2-エージェント・チャットを開始します。
AG2 : ユーザガイド – 高度な概念 : オーケストレーション : 2-エージェント・チャット
作成 : クラスキャット・セールスインフォメーション
作成日時 : 09/06/2025
バージョン : v0.9.9
* 本記事は docs.ag2.ai の以下のページを独自に翻訳した上でまとめ直し、補足説明を加えています :
* サンプルコードの動作確認はしておりますが、必要な場合には適宜、追加改変しています。
* ご自由にリンクを張って頂いてかまいませんが、sales-info@classcat.com までご一報いただけると嬉しいです。
◆ お問合せ : 下記までお願いします。
- クラスキャット セールス・インフォメーション
- sales-info@classcat.com
- ClassCatJP
AG2 : ユーザガイド – 高度な概念 : オーケストレーション : 2-エージェント・チャット
2 つのエージェントのチャットは最も単純な会話パターン形式です。各々の ConversableAgent エージェントの initiate_chat メソッドを使用して 2-エージェント・チャットを開始します。
次の図は 2-エージェント・チャットがどのように動作するかを示しています。
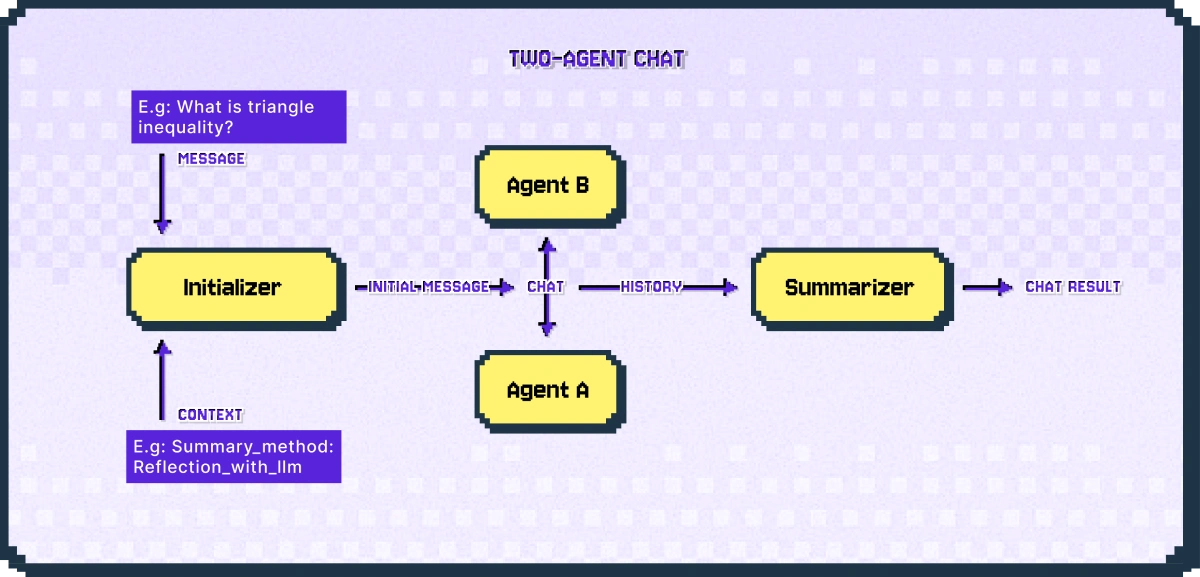
2-エージェント・チャットは 2 つの入力を受け取ります : メッセージ、これは呼び出し側 (caller) が提供する文字列です : コンテキスト、これはチャットの様々なパラメータを指定します。
送信者エージェントはチャット初期化メソッド (i.e., ConversableAgent の generate_init_message メソッド) を使用して入力から初期メッセージを生成し、それを受信者エージェントに送信してチャットを開始します。
送信者エージェントは、その initiate_chat メソッドが呼び出されるエージェントで、受信者エージェントは他方のエージェントです。
チャットが終了すれば、チャットの履歴はチャット summarizer により処理されます。summarizer はチャット履歴を要約して、チャットのトークン使用量を計算します。initiate_chat メソッドの summary_method パラメータを使用して要約のタイプを設定できます。デフォルトでは、チャットの最後のメッセージです (i.e, summary_method=’last_msg’)。
次の例は、学生エージェントと教師エージェント間の 2-エージェント・チャットです。その summarizer は LLM ベースの要約を使用しています。
import os
from autogen import ConversableAgent, LLMConfig
llm_config = LLMConfig(api_type="openai", model="gpt-5-nano")
#llm_config=LLMConfig({"api_type": "openai", "model": "gpt-5-nano", "api_key": os.environ["OPENAI_API_KEY"]})
student_agent = ConversableAgent(
name="Student_Agent",
system_message="あなたは学ぶ意欲のある学生です。",
llm_config=llm_config
)
teacher_agent = ConversableAgent(
name="Teacher_Agent",
system_message="あなたは数学の先生です。",
llm_config=llm_config
)
chat_result = student_agent.initiate_chat(
teacher_agent,
message="三角不等式とは何ですか?",
summary_method="reflection_with_llm",
max_turns=2,
)
出力例
Student_Agent (to Teacher_Agent):
三角不等式とは何ですか?
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
Teacher_Agent (to Student_Agent):
三角不等式とは、距離を測る空間で成り立つ基本的な不等式です。
- もう少しかんたんに言うと
どんな3点 A, B, C に対しても d(A,B) ≤ d(A,C) + d(C,B) が成り立ちます。
つまり A から B へ直線で行く距離は、途中を C を経由して行く距離より小さい、または等しいということです。
- ユークリッド平面での例
AB ≤ AC + BC(A, B, C は平面上の点)。
等号が成り立つときは C が AB 上の点で A と B の間にある場合です。つまり A, C, B が一直線上に並んで C が A と B の間にあるとき、AB = AC + CB になります。
例
- A = (0,0), B = (3,0), C = (2,0) のとき
AB = 3, AC = 2, BC = 1, 3 = 2 + 1(等号成立)。
- A = (0,0), B = (3,4), C = (1,2) のとき
AB = 5, AC ≈ 2.236, BC ≈ 2.828, AC + BC ≈ 5.064 > AB(不等号が等しくない)。
- 実用的な補足
実数のときの同値な形として |a + b| ≤ |a| + |b| も三角不等式です。等号が成立するのは、実数の場合は a と b が同符号のとき(または一方が 0 のとき)です。
- まとめ
三角不等式は「直線距離は、途中を経由するときの距離の和より小さい」という直感を、厳密に表したものです。
もし解き方の証明や他の空間での一般化(ノルム空間での ||x+y|| ≤ ||x|| + ||y|| など)を知りたい場合、希望を教えてください。
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
Student_Agent (to Teacher_Agent):
いいですね。証明の流れを1つ紹介します。
- ユークリッド空間のノルムを内積で定義します。||x|| = sqrt(⟨x, x⟩) とします。
- まず ||x+y||^2 = ⟨x+y, x+y⟩ = ||x||^2 + 2⟨x, y⟩ + ||y||^2 です。
- コーシー・シュワルツの不等式より |⟨x, y⟩| ≤ ||x|| ||y|| なので 2⟨x, y⟩ ≤ 2||x|| ||y||。
- よって ||x+y||^2 ≤ ||x||^2 + 2||x|| ||y|| + ||y||^2 = (||x|| + ||y||)^2。
- 両辺の平方根を取ると、||x+y|| ≤ ||x|| + ||y|| が得られます。
等号についての直感もひとつだけ:
- 等号が成立するのは、xとyが同じ方向(すなわち y が x の正のスカラー倍)である場合、または一方が0の場合です。
補足と generalization の道筋:
- ノルム空間の定義として、任意のベクトル空間での三角不等式 ||x+y|| ≤ ||x|| + ||y|| を要求することが多いです。これがノルムの公理の一つです。
- 内積空間ではコーシー・シュワルツを用いる証明があり、一般のノルム空間ではこれは公理として成り立つため、証明は空間の性質に依存します。
- 逆三角不等式も併せて覚えると便利です。すなわち ||x|| − ||y|| ≤ ||x−y|| です。
他に知りたいことを教えてください。次のリクエスト案:
- 内積空間だけでなく、一般のノルム空間での証明をもう少し詳しく。
- 逆三角不等式の証明と使い方。
- 距離空間の定義から三角不等式を導く別の視点。
- 練習問題(例題と解答付き)を用意する。
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
Teacher_Agent (to Student_Agent):
いいですね。以下に補足と generalization の道筋を、もう少し具体的に整理します。あわせて練習問題と解答案もつけます。
1) コーシー・シュワルツ不等式の完全な証明と等号条件
- 証明の定石: x, y を内積空間のベクトルとします。y ≠ 0 として
f(t) = ||x − t y||^2 ≥ 0 を考えると、
f(t) = ⟨x − t y, x − t y⟩ = ||x||^2 − 2t⟨x,y⟩ + t^2||y||^2
となる二次式です。これを t に関して最小化するときの最小値は非負です。
したがって判別式が負または等しい条件が必要で、
⟨x,y⟩^2 ≤ ||x||^2 ||y||^2 が得られ、これが
|⟨x,y⟩| ≤ ||x|| ||y|| すなわちコーシー・シュワルツ不等式です。
- 等号条件:
x, y がともに 0 でないとき等号が成立する必要十分条件は、x と y が同じ(非負のスカラー倍)方向にあることです。すなわち y = α x for some α ≥ 0。直感的には「同じ方向に重なるときだけ等号になる」ということです。
もし y = 0 や x = 0 の場合も等号は成立します。
2) 三角不等式のノルムへの適用と等号条件
- ユークリッド空間のノルムには ||x|| = sqrt(⟨x,x⟩) を用い、
||x+y||^2 = ||x||^2 + 2⟨x,y⟩ + ||y||^2
と書けます。コーシー・シュワルツより |⟨x,y⟩| ≤ ||x|| ||y|| なので
||x+y||^2 ≤ ||x||^2 + 2||x|| ||y|| + ||y||^2 = (||x|| + ||y||)^2
したがって ||x+y|| ≤ ||x|| + ||y|| が得られます。
- 等号条件の直感:
先ほどの等号条件を使うと、等号が成立するのは「x と y が同じ方向(y = α x, α ≥ 0)」の場合、または一方が 0 の場合です。
3) 一般のノルム空間への道筋
- 重要な点: 三角不等式 ||x+y|| ≤ ||x|| + ||y|| はノルムの公理の一つとして定義されます。したがって一般のノルム空間で三角不等式を “証明する” には、特定のノルムがどのように定義されているかによります。
- 典型的な一般化の道筋としては次の2つが挙げられます。
- 内積空間から生じるノルムの場合: コーシー・シュワルツを用いる証明が使えます。つまり内積の空間なら三角不等式は CS を使って導けます。
- p-ノルム(L^p など)やその他の具体的ノルム: Minkowski の不等式(三角不等式の一般化)を用いて証明します。例えば p ≥ 1 の場合
(|a1 + b1|^p + ... + |an + bn|^p)^{1/p} ≤ (|a1|^p + ... + |an|^p)^{1/p} + (|b1|^p + ... + |bn|^p)^{1/p}
を証明するのが一般的です。これには凸性やヤコビ・ブーリカの不等式などが使われます。
- 逆三角不等式も併せて覚えると便利です。すなわち
||x|| − ||y|| ≤ ||x − y|| です。
4) 距離空間からの別視点
- 距離空間の定義: 距離 d には三角不等式 d(x,z) ≤ d(x,y) + d(y,z) が必要です。距離関数からノルムを定義する場合、ノルム公理のうち三角不等式を満たすことが重要です。例えば d(x,y) = ||x − y|| を満たすとき、三角不等式は d の定義から自動的に得られます。
- 代替の直感: 「直線で結んだ距離は、途中の点を経由する距離の和より小さい」という直感は、距離関数の三角不等式で常に成り立つことを意味します。
5) 練習問題(解答つきの例題)
問題1
R^2 における標準ノルムで、x = (1, 2), y = (-3, 4) のとき
- ||x||, ||y||, ||x+y|| を計算して、三角不等式を検算せよ。
- 与えられた x, y に対して等号が成り立つかを判定せよ。
解答1
- ||x|| = sqrt(1^2 + 2^2) = sqrt(5)
- ||y|| = sqrt((-3)^2 + 4^2) = sqrt(25) = 5
- x + y = (-2, 6) ⇒ ||x+y|| = sqrt((-2)^2 + 6^2) = sqrt(40) = 2√10 ≈ 6.3249
- ||x|| + ||y|| = √5 + 5 ≈ 7.236
- 6.3249 ≤ 7.236 なので三角不等式は成立。等号は成立しない(角度は 0 度ではない)。
問題2
x, y ∈ R^n に対してコーシー・シュワルツ不等式を証明せよ(二次形式を用いず、x−ty のノルムの非負性から導く方法で)。
解答2
- y ≠ 0 として t ∈ R をとる。f(t) = ||x − t y||^2 ≥ 0。
f(t) = ||x||^2 − 2t⟨x,y⟩ + t^2||y||^2 という二次式。
この二次式の最小値は非負で、判別式が非負であるときに限る。
0 ≤ f(t) for all t implies discriminant ≤ 0:
(−2⟨x,y⟩)^2 − 4||y||^2||x||^2 ≤ 0 ⇒ ⟨x,y⟩^2 ≤ ||x||^2 ||y||^2.
これが |⟨x,y⟩| ≤ ||x|| ||y|| の証明。
問題3
x, y ∈ R^n が nonzero のとき、||x+y|| = ||x|| + ||y|| となる必要十分条件を述べよ。
解答3
- 内積空間の場合、等号が成立するのは x と y が同じ方向(y = α x, α ≥ 0)であること、あるいは片方が 0 の場合です。すなわち x と y が正のスカラー倍の関係にある場合のみ等号になる。
問題4
任意のノルム空間に対して、三角不等式が成り立つことを“公理”として受け取る場合、どういう性質を確認するとよいか。例として L^p 空間について簡単に述べよ。
解答4
- 三角不等式はノルムの公理のひとつであるため、対象ノルムがどのように定義されているかを確認します。
- 具体例として L^p 空間(1 ≤ p < ∞)では Minkowski 不等式により三角不等式を証明します。
- もし内積からノルムを定義している場合は CS 不等式を用いて三角不等式を導けます。
次のリクエスト案
- 内積空間だけでなく、一般のノルム空間での証明をもう少し詳しく
- 逆三角不等式の証明と使い方
- 距離空間の定義から三角不等式を導く別の視点
- 練習問題(解答付き)をさらに増やす
もし特に深掘りしたい「次のリクエスト案」があれば教えてください。たとえば
- Minkowski 不等式の証明を詳しく知りたい
- 逆三角不等式の厳密な等号条件を知りたい
- 練習問題をもう少し難しくして挑戦したい
のようなリクエストにも対応します。
--------------------------------------------------------------------------------
>>>>>>>> TERMINATING RUN (1e82a5fd-21e7-40c2-83d0-7391e38107e9): Maximum turns (2) reached
print(chat_result.summary)
出力例
- 三角不等式の基本形は d(x,y) ≤ d(x,z) + d(z,y) で、ノルム空間では d(x,y) = ||x−y|| を用いて ||x−y|| ≤ ||x−z|| + ||z−y||、特別な場合として ||x+y|| ≤ ||x|| + ||y|| がある。 - ユークリッド空間での証明の流れ:||x+y||^2 = ||x||^2 + 2⟨x,y⟩ + ||y||^2、コーシー・シュワルツ不等式 |⟨x,y⟩| ≤ ||x|| ||y|| より ||x+y||^2 ≤ (||x|| + ||y||)^2 となり、平方根を取って ||x+y|| ≤ ||x|| + ||y|| が得られる。 - 等号条件の直感:等号が成立するのは x と y が同じ方向にある場合(y = αx, α ≥ 0)またはどちらかが 0 の場合。 - 一般のノルム空間への道筋:内積空間では CS 不等式を用いて証明、一般のノルムでは Minkowski 不等式などを用いて証明・確認するのが一般。逆三角不等式も併せて覚えると便利。 - 距離空間の視点:d(x,y) = ||x−y|| が成り立つとき、三角不等式は距離関数の性質から自動的に得られる。 - 実践ポイント:CS の証明の理解、等号条件の把握、ノルム公理としての三角不等式の役割、Minkowski などの一般化の見取り図。 - 今回のやりとりの要点は以上。必要なら、内積空間の詳しい証明の別解や、Minkowski 不等式の証明、練習問題を追加で用意します。
上記の例では、summary メソッドは reflection_with_llm に設定されています、これは会話のメッセージのリストを受け取り、LLM への呼び出しを使用してこれらを要約します。
summary メソッドはまず受信者の LLM の使用を試み、それが利用可能でないならば送信者の LLM を使用します。このケースでは、受信者は “Teacher_Agent” で、送信者は “Student_Agent” です。
LLM への入力プロンプトは次のデフォルトプロンプトです :
print(ConversableAgent.DEFAULT_SUMMARY_PROMPT)
initiate_chat で summary_prompt 引数を設定することで、カスタムプロンプトを使用することもできます。
ChatResult オブジェクトには、会話履歴、人間の入力とトークンコストを含む、他の有用な情報も含まれます。
# Get the chat history.
import pprint
pprint.pprint(chat_result.chat_history)
以上
