単一ワークフローをエージェントにカプセル化する強力な手法が AG2 の nested チャットです。nested チャットは、ConversableAgent のプラグイン可能なコンポーネントである、nested チャット・ハンドラにより実現されます。
AG2 : ユーザガイド – 高度な概念 : オーケストレーション : Nested チャット
作成 : クラスキャット・セールスインフォメーション
作成日時 : 09/08/2025
バージョン : v0.9.9
* 本記事は docs.ag2.ai の以下のページを独自に翻訳した上でまとめ直し、補足説明を加えています :
* サンプルコードの動作確認はしておりますが、必要な場合には適宜、追加改変しています。
* ご自由にリンクを張って頂いてかまいませんが、sales-info@classcat.com までご一報いただけると嬉しいです。
◆ お問合せ : 下記までお願いします。
- クラスキャット セールス・インフォメーション
- sales-info@classcat.com
- ClassCatJP
AG2 : ユーザガイド – 高度な概念 : オーケストレーション : Nested チャット
単一ワークフローをエージェントにカプセル化する強力な手法が AG2 の nested チャットです。
Nested チャットが動作する方法
Nested チャットは、ConversableAgent のプラグイン可能なコンポーネントである、nested チャット・ハンドラにより実現されます。下の図は、メッセージを受信したときに、nested チャット・ハンドラが nested チャットのシークエンスをトリガーする仕組みを示しています。
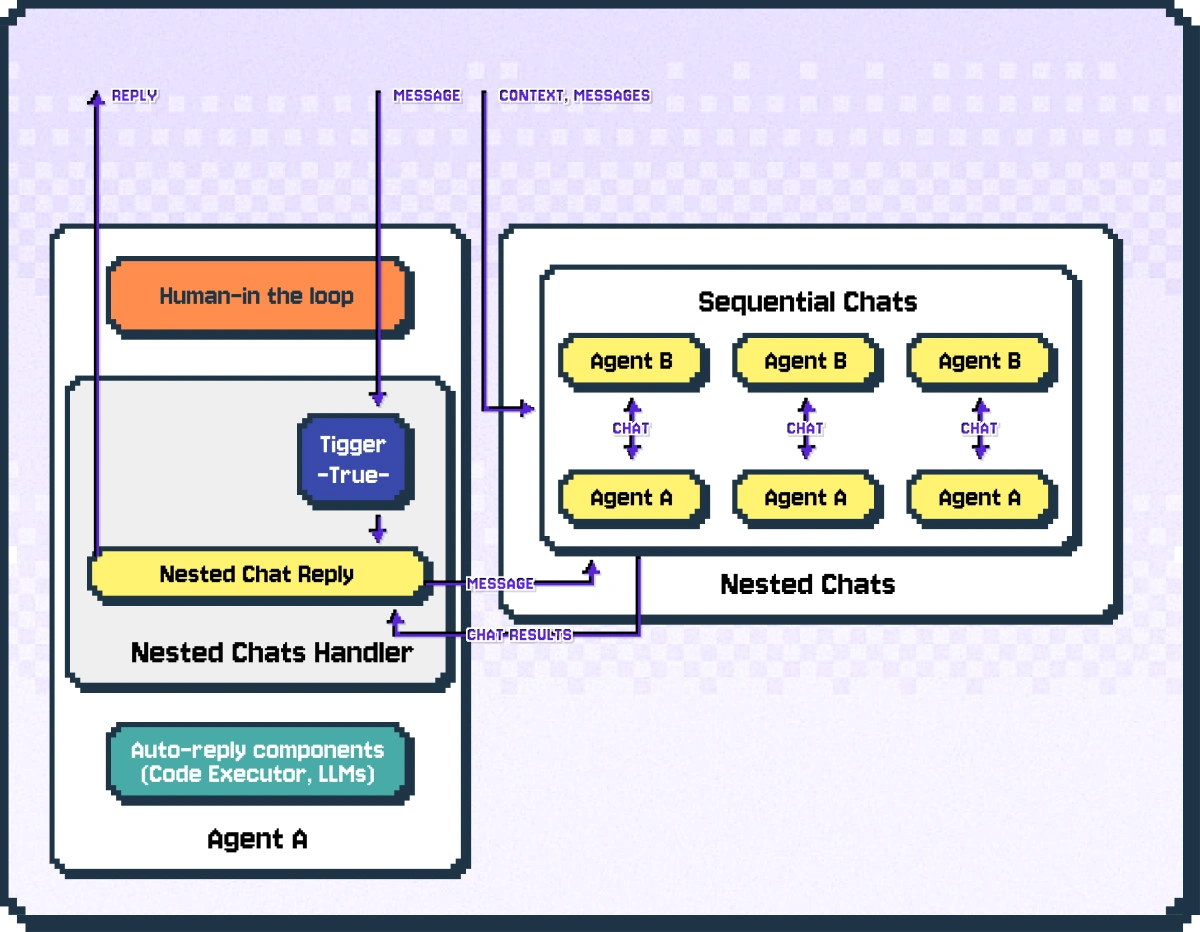
メッセージが届き、human-in-the-loop コンポーネントを通過すると、nested チャット・ハンドラは、ユーザにより指定された条件に基づいて、メッセージが nested チャットをトリガーするか確認します。
条件が満たされた場合、nested チャット・ハンドラは、シーケンシャル・チャット・パターンを使用して、指定された nested チャットのシークエンスを開始します。
nested チャットの各々について、送信エージェントは常に nested チャットをトリガーしたのと同じエージェントです。
最終的に、nested チャット・ハンドラは nested チャットの結果を使用して、元のメッセージ (デフォルトでは最後のチャットの要約) への応答を生成します。
例: 複雑なワークフローのカプセル化
ここでは、単一エージェント (lead_teacher_agent) が、他の 5 つのエージェントが関わるワークフローをカプセル化する、nested チャットを例示します。この内側のワークフローは 2-エージェントチャットとグループチャットを含みます。
結果は、このエージェントがチャットで返信のために呼び出されるとき、内部的には nested チャットを使用してワークフローを実行し、十分に検討された授業プランがその応答として返されます。
from autogen import ConversableAgent, GroupChatManager, GroupChat, LLMConfig
llm_config = LLMConfig({"api_type": "openai", "model": "gpt-5-nano"})
# カリキュラム基準 (Standards) エージェント
curriculum_agent = ConversableAgent(
name="Curriculum_Agent",
system_message="""あなたは4年生の教育のカリキュラム基準の専門家です。
トピックが与えられたとき、あなたはその学年に適した基準と学習目標を提示します。
すべてのレスポンスは以下の形式にフォーマットしてください:
基準:
- [基準1]
- [基準2]
目標:
- この授業の終わりまでに、生徒は [目標1] をできるようになる
- この授業の終わりまでに、生徒は [目標2] をできるようになる""",
human_input_mode="NEVER",
llm_config=llm_config,
)
# 授業プランナー・エージェント
lesson_planner_agent = ConversableAgent(
name="Lesson_Planner_Agent",
system_message="""あなたは授業プランニングの専門家です。
基準と目標が指定されたとき、以下を含む詳細な授業プランを作成します:
- 導入/つかみ(5〜10分)
- 主活動(20〜30分)
- 練習活動(15〜20分)
- 評価/まとめ(5〜10分)
明確な時間配分と必要な教材を示した構造化された授業プランとしてフォーマットしてください。""",
human_input_mode="NEVER",
llm_config=llm_config,
)
# 授業レビュー担当者・エージェント
lesson_reviewer_agent = ConversableAgent(
name="Lesson_Reviewer_Agent",
system_message="""あなたは授業プランのレビュー担当者です。以下の点を確認します:
1. 年齢に適した内容と活動である
2. 提示された基準との整合性がある
3. 時間配分が現実的である
4. 指示が明確である
5. 生徒の多様性に応じた学習機会がある
これらの観点で具体的なフィードバックを提供し、必要に応じて改善点を提案してください。""",
human_input_mode="NEVER",
llm_config=llm_config,
)
# 主任教師エージェント
lead_teacher_agent = ConversableAgent(
name="Lead_Teacher_Agent",
system_message="""あなたは4年生を担当する経験豊富な教師であり、授業プランニングのプロセス全体を監督します。
あなたの役割は以下です :
1. 明確なトピックをもってプランニングのプロセスを開始する
2. 他のエージェントからのフィードバックをレビューして、統合する
3. 最終的な授業プランが実践的で魅力的なものとなることを確実にする
4. 教室での経験に基づいて最終的な調整を行う""",
human_input_mode="NEVER",
llm_config=llm_config,
)
# 協働的な授業プラニングのためのグループチャットを作成
planning_chat = GroupChat(
agents=[curriculum_agent, lesson_planner_agent, lesson_reviewer_agent],
messages=[],
max_round=4,
send_introductions=True,
)
planning_manager = GroupChatManager(
groupchat=planning_chat,
llm_config=llm_config,
)
# 最終的な授業プランの標準形式へのフォーマッター
formatter_message = """あなたは授業プランのフォーマッターです。完成したプランを次の形式でフォーマットしてください:
授業プランのタイトル
扱う基準
主要な学習目標
必要な教材
授業プランの活動内容
評価の詳細
"""
lesson_formatter = ConversableAgent(
name="formatter_agent",
system_message=formatter_message,
llm_config=llm_config,
)
# nested チャット設定の作成
nested_chats = [
{
# 最初の内部チャットで、基準と目標を決定します。
# 改訂のラウンドは max_turns = 2 でサポートされます。
"recipient": curriculum_agent,
"message": lambda recipient, messages, sender, config: f"次のトピックについて、4年生向けの基準と目標を提示してください: {messages[-1]['content']}",
"max_turns": 2,
"summary_method": "last_msg",
},
{
# 続いてグループチャットが行われ、そこで授業プランが作成されます。
"recipient": planning_manager,
"message": "これらの基準と目標に基づいて、詳細な授業プランを作成してください。",
"max_turns": 1,
"summary_method": "last_msg",
},
{
# 最後に、2-エージェント・チャットが授業プランをフォーマットします。
# この結果が lead_teacher_agent の応答になります。
"recipient": lesson_formatter,
"message": "授業プランをフォーマットしてください。",
"max_turns": 1,
"summary_method": "last_msg",
}
]
# 主任教師により nested チャットを登録します。
lead_teacher_agent.register_nested_chats(
chat_queue=nested_chats,
trigger=lambda sender: sender not in [curriculum_agent, planning_manager, lesson_reviewer_agent],
)
# human-in-the-loop エージェント
human = ConversableAgent(
name="human_agent",
human_input_mode="ALWAYS"
)
# A two-agent chat between our human and the lead_teacher_agent
# to demonstrate the full workflow is within the one agent
result = lead_teacher_agent.initiate_chat(
recipient=human,
message="何のトピックのための授業プランをご希望ですか?",
max_turns=2
)
print("最終的な授業プラン:\n", result.summary)
出力例
Lead_Teacher_Agent (to human_agent):
何のトピックのための授業プランをご希望ですか?
--------------------------------------------------------------------------------
Replying as human_agent. Provide feedback to Lead_Teacher_Agent. Press enter to skip and use auto-reply, or type 'exit' to end the conversation: 算数
human_agent (to Lead_Teacher_Agent):
算数
--------------------------------------------------------------------------------
********************************************************************************
Starting a new chat....
********************************************************************************
Lead_Teacher_Agent (to Curriculum_Agent):
次のトピックについて、4年生向けの基準と目標を提示してください: 算数
--------------------------------------------------------------------------------
Curriculum_Agent (to Lead_Teacher_Agent):
基準:
- 整数の位取りと多桁の四則演算の計算力を身につけ、計算過程を明確に説明できる。
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行える。
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
--------------------------------------------------------------------------------
Lead_Teacher_Agent (to Curriculum_Agent):
以下は、4年生向けの算数トピック「多桁の整数の四則演算と分数の基礎」に対する、明確な基準と学習目標です。
- トピック名
多桁の整数の四則演算と分数の基礎(位取り・筆算の計算過程の説明、等価分数の識別、および同分母の分数の加減)
- 基準(学習基準/評価基準)
1) 整数の位取りと多桁の四則演算の計算力を身につけ、計算過程を明確に説明できること
- 例: 筆算の各段階を言語化し、なぜその手順になるのかを説明できる
- 例: 位取りの扱い(繰り上がり・繰り下がり)を正確に適用できる
2) 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
- 例: 2つの分数が等価かどうかを判断できる
- 例: 同分母の分数の分子を足し引きして正しい和・差を求められる
- 目標(学習目標 / 成果指標)
1) この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- 具体的表現例: 「この計算はなぜこの順序で進めるべきか」「繰り上がり/繰り下がりをどのように処理したかを、段階ごとに言葉で説明できる」
2) この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
- 具体的表現例: 「2つの分数が等しい理由を、分子・分母の関係を用いて説明できる」「同分母の分数の加減を、分子だけを操作して正しい答えを得られる」
- 教師用の補足(実践の観点からのヒント)
- 成果の観察指標: 生徒が自分の解法を口頭・筆記で説明できるか、解答の途中経過を図や言葉で再現できるかを観察する
- 形成的評価のアイデア: 短い口頭説明のスキャフォールド(例文フレーム)を用意する。例: 「まずは…の理由でここを計算します。次に…、最後に…になります。」
- 差別化の観点: 計算の基本が不安定な生徒には、桁ごとの計算手順を視覚化できる材料(位取りブロック、十進数ボード、分数棒など)を活用する
- 学習を支える語彙サポート: 「位取り」「繰り上がり」「約分」「等価」「同分母」「分子」「分母」などの用語を日常的に使う練習を組み込む
この基準と目標は、授業計画の出発点として、評価設計(形成的評価と総括的評価の設計)、教材・活動の選択、差別化戦略の設計につなげやすい形式になっています。必要に応じて、具体的な活動案、例題、評価チェックリストも追加でご提供します。
--------------------------------------------------------------------------------
Curriculum_Agent (to Lead_Teacher_Agent):
基準:
- 整数の位取りと多桁の四则演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
--------------------------------------------------------------------------------
>>>>>>>> TERMINATING RUN (b848b42c-2b0c-4020-97c5-fb42b04842e8): Maximum turns (2) reached
********************************************************************************
Starting a new chat....
********************************************************************************
Lead_Teacher_Agent (to chat_manager):
これらの基準と目標に基づいて、詳細な授業プランを作成してください。
Context:
基準:
- 整数の位取りと多桁の四则演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
--------------------------------------------------------------------------------
Next speaker: Lesson_Planner_Agent
Lesson_Planner_Agent (to chat_manager):
基準:
- 整数の位取りと多桁の四則演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
授業計画(60分想定)
対象学年/科目: 小学校4年生 算数
1) 導入/つかみ(5〜10分) 7分
- 活動内容
- 身近な場面の問題提示: 「お買い物の合計金額を計算する場面を想像してみよう。4桁の金額が2つあるとして、正しく位取りを合わせて計算するにはどうするか考える。」
- 黒板に例題を提示: 4桁同士の足し算(例: 2,674 + 1,945)を見せ、解法の根拠を口頭で説明させる前提を作る。
- 学習者同士の短い会話 therapy: ペアで「この計算でどの位の計算をしているか」「なぜこの位までそろえるのか」を短く言い合う。
- 教材/準備物
- 黒板/ホワイトボード、マーカーペン
- 例題カード(2〜3問の4桁同士の足し算、引き算の導入例)
- 置き換え用の数直線・位取りマット(必要に応じて)
- 教師の支援ポイント
- 生徒が自分の言葉で「位取りの理由」を説明できるように、具体的な語彙とフレーム(例: 「この位の和は…、なぜなら…だからです」)を用意しておく。
2) 主活動(20〜30分) 25分
- 活動1: 整数の位取りと多桁の四則演算の計算過程の明確な説明(約12〜14分)
- 内容
- 加算の長算の模擬演習を教師がデモ
- 例題: 2,674 + 1,945
- 手順の明示
1) 問題を読み、数を位にそろえる
2) 各位の和/差を計算し、桁上がり/繰り上がりを説明
3) 解の根拠を言語化(「この位で繰り上がったのはなぜか」)
4) 確認のチェックリストを用いて再確認
- 学習者の活動
- ペアで1問ずつ解き、解法の根拠を相手に説明する
- 教師は観察カードを用いて、 reasoning の質をチェック
- 教材/準備物
- 黒板用の例題、演算手順カード
- 置き換え可能な基礎十進ブロック/位取りマット(実物教材がある場合)
- 活動2: 分数の基本概念・等価分数の識別・同分母の加減(約12〜14分)
- 内容
- 等価分数の識別
- フラグメント/分数ブロックを使い、3/4 と 6/8 が等価であることを視覚的に示す
- 小グループで等価性を説明させる
- 同分母の分数の加減
- 例題: 3/4 + 1/4、2/5 + 1/5(共通分母がそのまま分子の和になる例)
- フレームワーク提示
- 1) 分母は揃える
- 2) 分子を足し引きする
- 3) 結果を簡約できる場合は簡約する
- 学習者の活動
- 分数ブロックを使って等価分数を作り、異なる表現が同じ量を表すことを説明
- 共有分母での加減を計算し、答えの妥当性を説明
- 教材/準備物
- 分数教材(分数円・分数ブロック、分数カード)
- 黒板/ホワイトボード、マーカー
- 指導のヒント
- 学習の差を埋めるためのヒントを用意(例: 文章フレーム「理由は…だからです」/「最初に共通分母を作る理由は…」)
- 困難な生徒にはサポート付きの解法手順カードを提供
3) 練習活動(15〜20分) 18分
- 内容
- 整数の練習問題(3問〜4問)
- 例: 4桁同士の加算・減算・掛け算・長割り算の問題(例: 2,468 + 3,579、9,210 - 4,373、134 × 27、1,284 ÷ 12)
- 各問題の横に「解法の根拠を書く」スペースを用意
- 分数の練習問題(3問〜4問)
- 等価分数の識別問題
- 例: 3/4 と 6/8 は等価か?根拠を書かせる
- もう1問: 5/10 と 1/2 は等価か?理由
- 同分母の加減
- 例: 3/4 + 1/4、2/5 + 1/5、7/9 - 2/9
- 学習者の活動
- ペアで解答を交換し、相互に解法の根拠を確認
- 教師は回収カードやチェックリストで進度を確認
- 教材/準備物
- ワークシート(多桁の算算問題と分数問題のセット)
- 解法の根拠記入欄つき
- 答え合わせ用の答えキー
4) 評価/まとめ(5〜10分) 7分
- 内容
- 終了時の短い評価(exit ticket)
- 問題1: 多桁の整数の計算問題を1問解き、解法の根拠を1文で説明
- 問題2: 等価分数の識別1問と、同分母の加減の1問を解く
- 教師のフィードバック
- どの学習者が解法の根拠を口頭で説明できたか、どの学習者が等価分数の識別に課題があるかを短いメモとして記録
- 教材/準備物
- Exit ticket用紙
- 簡易評価チェックリスト(根拠の明示、等価性の識別、同分母の計算の正確さを評価)
- 学習の多様性への対応
- 難易度調整: 基本の問題と拡張問題を用意、学習遅れの生徒には追加サポート(解法のフレーム、手順カード、ペア支援)
- 言語サポート: 文章フレームを提供、聴覚的に説明する機会を増やす
- 学習スタイルの違いに対応: 視覚的教材、聴覚的説明、書字による説明の3コードで説明機会を提供
必要な教材・準備
- 基本教材
- 黒板/ホワイトボード、マーカー
- 基本十進ブロック、位取りマット(整数の位取り練習用)
- 分数ブロック/円、分数カード
- 置き換え可能な演習用ワークシート(多桁算算、分数の練習問題)
- 例題カードと解法のフレーム(根拠の書き方ガイド)
- 補助教材
- 言語サポート用の文章フレームカード
- exit ticket用紙と評価チェックリスト
- 技術的準備
- デジタル投影機/スマートボードが利用できる場合は、解法のデモ動画や解説スライドを用意
評価の観点(学習の形成的評価)
- 整数の位取り・四則演算
- 位取り合わせの正確さ
- 計算過程の説明の明瞭さ
- 分数
- 等価分数の識別能力
- 同分母の加減の正確さと手順の妥当性
- 表現力・語彙
- 解法の根拠を明確に言語化できるか
- 差異対応
- 学習困難な生徒への適切な支援の提供と、学習の伸びを促す環境づくり
補足
- このプランは4年生の「整数の位取りと多桁の四則演算」および「分数の基本概念・等価分数・同分母の加減」という2つの基準・目標に対応する構成です。時間配分は各セクションの範囲内に収まるように設定しています。必要に応じて、特定のクラスの学習状況に合わせて難易度を微調整してください。
--------------------------------------------------------------------------------
Next speaker: Lesson_Reviewer_Agent
Lesson_Reviewer_Agent (to chat_manager):
以下は、基準と目標に基づいた詳細な授業プラン(60分想定)です。対象は小学校4年生、算数です。
- 基準:
- 整数の位取りと多桁の四則演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
- 目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
授業計画(60分想定)
対象学年/科目: 小学校4年生 算数
1) 導入/つかみ(7分)
- 活動内容
- 身近な場面の問題提示: 「お買い物の合計金額を計算する場面を想像してみよう。4桁の金額が2つあるとして、正しく位取りを合わせて計算するにはどうするか考える。」
- 黒板に例題を提示: 4桁同士の足し算(例: 2,674 + 1,945)を見せ、解法の根拠を口頭で説明させる前提を作る。
- 学習者同士の短い会話: ペアで「この計算でどの位の計算をしているか」「なぜこの位までそろえるのか」を短く言い合う。
- 教材/準備物
- 黒板/ホワイトボード、マーカーペン
- 例題カード(2〜3問の4桁同士の足し算、引き算の導入例)
- 置き換え用の数直線・位取りマット(必要に応じて)
- 教師の支援ポイント
- 学習者が自分の言葉で「位取りの理由」を説明できるように、具体的な語彙とフレーム(例: 「この位の和は…、なぜなら…だからです」)を用意しておく。
2) 主活動(25分)
- 活動1: 整数の位取りと多桁の四則演算の計算過程の明確な説明(約12–14分)
- 内容
- 加算の長算の模擬演習を教師がデモ
- 例題: 2,674 + 1,945
- 手順の明示
1) 問題を読み、数を位にそろえる
2) 各位の和/差を計算し、桁上がり/繰り上がりを説明
3) 解の根拠を言語化(「この位で繰り上がったのはなぜか」)
4) 確認のチェックリストを用いて再確認
- 学習者の活動
- ペアで1問ずつ解き、解法の根拠を相手に説明する
- 教師は観察カードを用いて、 reasoning の質をチェック
- 教材/準備物
- 黒板用の例題、演算手順カード
- 置き換え可能な基礎十進ブロック/位取りマット(実物教材がある場合)
- 活動2: 分数の基本概念・等価分数の識別・同分母の加減(約12–14分)
- 内容
- 等価分数の識別
- フラグメント/分数ブロックを使い、3/4 と 6/8 が等価であることを視覚的に示す
- 小グループで等価性を説明させる
- 同分母の分数の加減
- 例題: 3/4 + 1/4、2/5 + 1/5(共通分母がそのまま分子の和になる例)
- フレームワーク提示
- 1) 分母は揃える
- 2) 分子を足し引きする
- 3) 結果を簡約できる場合は簡約する
- 学習者の活動
- 分数ブロックを使って等価分数を作り、異なる表現が同じ量を表すことを説明
- 共有分母での加減を計算し、答えの妥当性を説明
- 教材/準備物
- 分数教材(分数円・分数ブロック、分数カード)
- 黒板/ホワイトボード、マーカー
- 指導のヒント
- 学習の差を埋めるためのヒントを用意(例: 文章フレーム「理由は…だからです」/「最初に共通分母を作る理由は…」)
- 困難な生徒にはサポート付きの解法手順カードを提供
3) 練習活動(18分)
- 内容
- 整数の練習問題(3問〜4問)
- 例: 4桁同士の加算・減算・掛け算・長割り算の問題(例: 2,468 + 3,579、9,210 - 4,373、134 × 27、1,284 ÷ 12)
- 各問題の横に「解法の根拠を書く」スペースを用意
- 分数の練習問題(3問〜4問)
- 等価分数の識別問題
- 例: 3/4 と 6/8 は等価か?根拠を書かせる
- もう1問: 5/10 と 1/2 は等価か?理由
- 同分母の加減
- 例: 3/4 + 1/4、2/5 + 1/5、7/9 - 2/9
- 学習者の活動
- ペアで解答を交換し、相互に解法の根拠を確認
- 教師は回収カードやチェックリストで進度を確認
- 教材/準備物
- ワークシート(多桁の算算問題と分数問題のセット)
- 解法の根拠記入欄つき
- 答え合わせ用の答えキー
4) 評価/まとめ(5–10分)
- 内容
- 終了時の短い評価(exit ticket)
- 問題1: 多桁の整数の計算問題を1問解き、解法の根拠を1文で説明
- 問題2: 等価分数の識別1問と、同分母の加減の1問を解く
- 教師のフィードバック
- どの学習者が解法の根拠を口頭で説明できたか、どの学習者が等価分数の識別に課題があるかを短いメモとして記録
- 教材/準備物
- Exit ticket用紙
- 簡易評価チェックリスト(根拠の明示、等価性の識別、同分母の計算の正確さを評価)
- 学習の多様性への対応
- 難易度調整: 基本の問題と拡張問題を用意、学習遅れの生徒には追加サポート(解法のフレーム、手順カード、ペア支援)
- 言語サポート: 文章フレームを提供、聴覚的に説明する機会を増やす
- 学習スタイルの違いに対応: 視覚的教材、聴覚的説明、書字による説明の3コードで説明機会を提供
必要な教材・準備
- 基本教材
- 黒板/ホワイトボード、マーカー
- 基本十進ブロック、位取りマット(整数の位取り練習用)
- 分数ブロック/円、分数カード
- 置き換え可能な演習用ワークシート(多桁算算、分数の練習問題)
- 例題カードと解法のフレーム(根拠の書き方ガイド)
- 補助教材
- 言語サポート用の文章フレームカード
- exit ticket用紙と評価チェックリスト
- 技術的準備
- デジタル投影機/スマートボードが利用できる場合は、解法のデモ動画や解説スライドを用意
評価の観点(形成的評価の観点)
- 整数の位取り・四則演算
- 位取り合わせの正確さ
- 計算過程の説明の明瞭さ
- 分数
- 等価分数の識別能力
- 同分母の加減の正確さと手順の妥当性
- 表現力・語彙
- 解法の根拠を明確に言語化できるか
- 差異対応
- 学習困難な生徒への適切な支援の提供と、学習の伸びを促す環境づくり
補足
- このプランは4年生の「整数の位取りと多桁の四則演算」および「分数の基本概念・等価分数・同分母の加減」という2つの基準・目標に対応する構成です。時間配分は各セクションの範囲内に収まるように設定しています。クラスの実情に応じて難易度の微調整やサポート戦略を追加してください。
もし、特定のクラスの実情(遅れがちな生徒の人数、英語・言語サポートのニーズ、教具の入手可否など)が分かれば、それに合わせて微調整案もご提案します。
--------------------------------------------------------------------------------
Next speaker: Curriculum_Agent
Curriculum_Agent (to chat_manager):
基準:
- 年齢に適した内容と活動であるが、長算の模擬演習は4年生にとってやや高度な場面も含むため、基礎となる位取りの操作を先に確実に定着させる段階を設け、計算過程の言語化をサポートする具体的な語彙フレームを追加するとよい。
- 提示された基準との整合性は高いが、各活動がどの基準にどの要素で対応しているかの対応表(マッピング)を授業計画の冒頭に添えると、評価者にも教員にも理解が深まりやすい。
- 時間配分はおおむね現実的だが、導入と指示→演示→協働→個別練習の移行に要する時間差が生じやすいため、何分間で何を完了させるかの明確なタイムボックスと遷移のテンプレートを追加すると安定する。
- 指示が比較的明確であるが、全生徒が同じ速度で理解できるとは限らないため、基準ごとに「達成条件の下位互換(サポートあり)/ 上位互換(挑戦課題)」を明記すると、現場での柔軟な対応が取りやすくなる。
- 学習の多様性への対応は一定程度盛り込まれているが、ELL・特別支援教育を受ける児童、学習遅滞児、早期完成児などの具体的な支援戦略を、教材例・言語フレーム・タスク分岐としてより詳しく盛り込むと効果が高まる。
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
改善の提案(具体的な微調整案)
- 学習段階の明確化と時間の安定化
- 導入5分、活動1(位取りと長算デモ)15分、活動2(分数の等価・加減)15分、練習15分、評価5分、合計55分程度の厳密なタイムボックスを設定し、遷移の定型手順を用意する。
- 活動1と活動2の前後に「短い確認クイズ」や「口頭のチェックリスト」を挟み、理解度の早期把握を行う。
- 明確な評価基準とフィードバック
- 各セクションに対して、達成度を判定する指標を3段階程度で設定(例: 基本的理解/十分な説明/高度な説明)し、 exit ticket の採点基準と結びつける。
- 解法の根拠を言語化する際の最低語数や表現例を教師用サンプルとして提供する。
- 学習の多様性への具体的な対応
- 言語サポート: 文章フレームカードを複数用意し、説明が苦手な生徒には文字と図を併用した「図解ベースの説明フレーム」を提供。
- 困難さに応じた分岐タスク
- 基本レベル: 4桁の加算・減算、同分母の簡単な加減のみを扱う。
- 拡張レベル: 2桁×2桁の乗算、分数の簡約を組み合わせた応用問題、複数ステップの分数問題を追加。
- 学習遅れの生徒への支援
- 基礎の位取りカード、手元の操作ガイド、ペアワークでの1対1指導などを追加。
- 指示と進行の明確化
- 各活動のゴールをカード形式で提示し、生徒が終えるべき成果物を視覚的に把握できるようにする。
- 教師用の「指示テンプレート」を用意し、同じ言い回しで生徒へ伝えられるよう統一する。
- 教具と教材の活用の強化
- 位取りマット・十進ブロック・分数ブロックを具体的な操作手順と結びつけ、デモ→体験→説明の順で進める流れを明確化する。
- デジタル補助を使える場合、デモ動画または解法スライドを活用して視覚的理解を補強する。
- 実務的コメント
- 実際のクラス規模・学習ニーズに応じて、活動2の等価分数の例を複数レベル用意し、ペアの組み替えを頻繁に行い多様な視点から学習を促す。
- exit ticket による形成的評価を、授業終了直後だけでなく翌日以降の短い復習機会にも結びつけると、習得定着を高められる。
このままの計画を実施する場合の運用上の留意点
- 事前に生徒の算数における強みと苦手を把握し、クラス全体の難易度を適切に設定する。
- 各セクションの終わりに短い「理解度のリフレクション」を設け、教師が次回計画に反映できるようにする。
- 言語サポートと視覚教材の併用を徹底し、第三言語指導が必要な生徒にも配慮する。
もし、特定のクラスの実情(遅れがちな生徒の人数、英語・言語サポートのニーズ、教具の入手可否など)が分かれば、それに合わせて微調整案もご提案します。
--------------------------------------------------------------------------------
>>>>>>>> TERMINATING RUN (6305a946-1382-4125-883b-aa2c9b01beaa): Maximum rounds (4) reached
>>>>>>>> TERMINATING RUN (b86824d3-8df8-4a8a-a95f-2c371bad3394): Maximum turns (1) reached
********************************************************************************
Starting a new chat....
********************************************************************************
Lead_Teacher_Agent (to formatter_agent):
授業プランをフォーマットしてください。
Context:
基準:
- 整数の位取りと多桁の四则演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
これらの基準と目標に基づいて、詳細な授業プランを作成してください。
Context:
基準:
- 整数の位取りと多桁の四则演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
目標:
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
--------------------------------------------------------------------------------
>>>>>>>> USING AUTO REPLY...
formatter_agent (to Lead_Teacher_Agent):
<title>多桁の整数の四則演算と分数の基礎(等価分数と同分母の加減)</title>
<standards>
- 整数の位取りと多桁の四則演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
</standards>
<learning_objectives>
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
</learning_objectives>
<materials>
- 白板・マーカーまたはホワイトボード、プロジェクター
- 位取りマップ/位取りカード、基尺ブロック(10のまとまり、1のまとまりなど)
- 演算プリント(多桁の整数の足し算・引き算・掛け算の練習問題、解法の根拠を説明させる設問付き)
- 分数の教材(分数棒、分数円、等価分数カード、同分母の加減の練習問題)
- 筆記用具、ノート
</materials>
<activities>
- 導入とウォームアップ(5–7分)
- 日常場面の話題から「大きな数の計算が必要な理由」を短く確認。
- これから解く問題の方針を5つの質問バンクとして提示し、生徒に自分の考えを1–2文で説明させる。
- 学習活動A:多桁の整数の四則演算(位取りと計算過程の説明を重視)(20–25分)
1) 教師デモ(5–7分)
- 3456 + 7891 の計算過程を位取りカードと基尺ブロックを用いて示す。各段階で何を計算しているか、なぜその順番になるのかを声に出して説明する。
- 例: 桁の揃え、仮の答え、繰り上がり/繰り下がりの理由、答えの検算方法を解説。
2) 学習者活動(10–12分)
- 生徒ペアで同様の問題を解く(例: 2487 + 5329、7046 − 2194)。
- 各自の解法をノートに書き、ペアの相手に根拠付きで説明させる。教師は各ペアを巡回し、説明の妥当性を観察。
3) 共有・振り返り(5分)
- いくつかの解法を全体で共有。誤りが出やすいポイント(繰り上がり・繰り下がり、位取りの揃え方、検算の方法)を再確認。
- 学習活動B:分数の基礎・等価分数の識別(15–20分)
1) 教師デモ(5分)
- 2/3 と 4/6 の等価性を分数棒・分数円で可視化。等価分数の考え方(分子・分母に同じ数を掛け/割ると等しくなる)を言語化。
2) 学習者活動(10–12分)
- 等価分数カードを使って、他の分数の等価片を作る練習(例: 5/8 の等価分数を作る、3/9 の等価分母化など)。
- ペアで見つけた等価分数を説明させ、なぜ等価になるのかを根拠付きで述べさせる。
3) 共有・振り返り(3–5分)
- 生徒の説明を全体で確認し、等価の判定に用いる基準を再確認。
- 学習活動C:同分母の分数の加減(12–18分)
1) 練習問題提示(教師)
- 例: 3/8 + 5/8、7/12 − 3/12、1/4 + 1/4 など、同分母の場合の計算手順を提示。
2) 個別・ペア作業(10–12分)
- 同分母の分数の加減を練習問題(4問程度)に取り組む。答えだけでなく、分母はそのまま、分子の計算をどう行ったかを説明させる。
3) 共有・フィードバック(3–4分)
- 解法の説明の質を振り返り、分数の表現の揺れ(約分の有無、最終的な形の確認)を整える。
- まとめと自習案内(5–7分)
- 今回の授業の要点を再確認。多桁演算の「計算過程を説明する力」と、分数の「等価判定と同分母の加減」を意識して学習ノートに短い要約を書く。
- 宿題案内:同様の問題を家庭で3問ずつ練習。追加チャレンジとして、2つの異なる同分母の分数の和差を求め、解法の根拠を1文で説明する。
</activities>
<assessment>
- 形成的評価の観点
- 計算過程の説明の明確さ:各段階で何を計算しているか、なぜその操作を選んだかを生徒が説明できるか。
- 正確性:解答が正しく、位取り・繰り上がり/繰り下がり・検算の有無が適切か。
- 戦略の活用:筆算だけでなく、位取り表・検算・推測値の活用など、適切な戦略を選択して説明できるか。
- 分数の理解:等価分数を正しく識別できるか、同分母の加減計算が正確か。
- 評価手法
- 演習プリントの採点と解法の根拠説明の観察記録
- ペアワーク時の口頭説明の評価
- 授業末のエグジットチケット(短い問題セット)を用いた即時フィードバック
- エグジットチケットの例
- 問題1: 4桁の数 3456 + 7891 の答えと、どの桁で繰り上がりが起きたかを説明せよ。
- 問題2: 2/5 と 4/10 は等価か。等価であれば理由を述べよ。
- 問題3: 同分母 7/9 + 2/9 を計算し、最終的な約分が必要かどうかを判断して答えを示せ。
- 問題4: 5/8 + 3/8 の計算過程を説明し、最終形を示せ。
- フォローアップ
- 学習が遅れている生徒には、個別の補習プリントと個別の説明タイムを設定。先取り学習として、より大きい数の同様の練習問題を追加する。
</assessment>
--------------------------------------------------------------------------------
最終的な授業プラン:
<title>多桁の整数の四則演算と分数の基礎(等価分数と同分母の加減)</title>
<standards>
- 整数の位取りと多桁の四則演算の計算力を身につけ、計算過程を明確に説明できること
- 分数の基本概念を理解し、等価分数の識別と、同分母の分数の加減を正しく行えること
</standards>
<learning_objectives>
- この授業の終わりまでに、生徒は多桁の整数の四則演算を正確に解くことができ、解法の根拠を説明できるようになる
- この授業の終わりまでに、生徒は分数の等価分数を識別し、同分母の分数の加減を正しく計算できるようになる
</learning_objectives>
<materials>
- 白板・マーカーまたはホワイトボード、プロジェクター
- 位取りマップ/位取りカード、基尺ブロック(10のまとまり、1のまとまりなど)
- 演算プリント(多桁の整数の足し算・引き算・掛け算の練習問題、解法の根拠を説明させる設問付き)
- 分数の教材(分数棒、分数円、等価分数カード、同分母の加減の練習問題)
- 筆記用具、ノート
</materials>
<activities>
- 導入とウォームアップ(5–7分)
- 日常場面の話題から「大きな数の計算が必要な理由」を短く確認。
- これから解く問題の方針を5つの質問バンクとして提示し、生徒に自分の考えを1–2文で説明させる。
- 学習活動A:多桁の整数の四則演算(位取りと計算過程の説明を重視)(20–25分)
1) 教師デモ(5–7分)
- 3456 + 7891 の計算過程を位取りカードと基尺ブロックを用いて示す。各段階で何を計算しているか、なぜその順番になるのかを声に出して説明する。
- 例: 桁の揃え、仮の答え、繰り上がり/繰り下がりの理由、答えの検算方法を解説。
2) 学習者活動(10–12分)
- 生徒ペアで同様の問題を解く(例: 2487 + 5329、7046 − 2194)。
- 各自の解法をノートに書き、ペアの相手に根拠付きで説明させる。教師は各ペアを巡回し、説明の妥当性を観察。
3) 共有・振り返り(5分)
- いくつかの解法を全体で共有。誤りが出やすいポイント(繰り上がり・繰り下がり、位取りの揃え方、検算の方法)を再確認。
- 学習活動B:分数の基礎・等価分数の識別(15–20分)
1) 教師デモ(5分)
- 2/3 と 4/6 の等価性を分数棒・分数円で可視化。等価分数の考え方(分子・分母に同じ数を掛け/割ると等しくなる)を言語化。
2) 学習者活動(10–12分)
- 等価分数カードを使って、他の分数の等価片を作る練習(例: 5/8 の等価分数を作る、3/9 の等価分母化など)。
- ペアで見つけた等価分数を説明させ、なぜ等価になるのかを根拠付きで述べさせる。
3) 共有・振り返り(3–5分)
- 生徒の説明を全体で確認し、等価の判定に用いる基準を再確認。
- 学習活動C:同分母の分数の加減(12–18分)
1) 練習問題提示(教師)
- 例: 3/8 + 5/8、7/12 − 3/12、1/4 + 1/4 など、同分母の場合の計算手順を提示。
2) 個別・ペア作業(10–12分)
- 同分母の分数の加減を練習問題(4問程度)に取り組む。答えだけでなく、分母はそのまま、分子の計算をどう行ったかを説明させる。
3) 共有・フィードバック(3–4分)
- 解法の説明の質を振り返り、分数の表現の揺れ(約分の有無、最終的な形の確認)を整える。
- まとめと自習案内(5–7分)
- 今回の授業の要点を再確認。多桁演算の「計算過程を説明する力」と、分数の「等価判定と同分母の加減」を意識して学習ノートに短い要約を書く。
- 宿題案内:同様の問題を家庭で3問ずつ練習。追加チャレンジとして、2つの異なる同分母の分数の和差を求め、解法の根拠を1文で説明する。
</activities>
<assessment>
- 形成的評価の観点
- 計算過程の説明の明確さ:各段階で何を計算しているか、なぜその操作を選んだかを生徒が説明できるか。
- 正確性:解答が正しく、位取り・繰り上がり/繰り下がり・検算の有無が適切か。
- 戦略の活用:筆算だけでなく、位取り表・検算・推測値の活用など、適切な戦略を選択して説明できるか。
- 分数の理解:等価分数を正しく識別できるか、同分母の加減計算が正確か。
- 評価手法
- 演習プリントの採点と解法の根拠説明の観察記録
- ペアワーク時の口頭説明の評価
- 授業末のエグジットチケット(短い問題セット)を用いた即時フィードバック
- エグジットチケットの例
- 問題1: 4桁の数 3456 + 7891 の答えと、どの桁で繰り上がりが起きたかを説明せよ。
- 問題2: 2/5 と 4/10 は等価か。等価であれば理由を述べよ。
- 問題3: 同分母 7/9 + 2/9 を計算し、最終的な約分が必要かどうかを判断して答えを示せ。
- 問題4: 5/8 + 3/8 の計算過程を説明し、最終形を示せ。
- フォローアップ
- 学習が遅れている生徒には、個別の補習プリントと個別の説明タイムを設定。先取り学習として、より大きい数の同様の練習問題を追加する。
</assessment>
以上
